Der Knobelthread

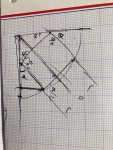
[willi.k]

@willi.k man kann ein Dreieck finden, eine Seite ist der Radius des Kreises, ein die anderen Seiten sind Teil des Quadrates bzw. darauf abbildbar …

mir dämmert was, ich bekomm's aber nicht gebacken... außerdem gibt's jetzt erstmal Gänsleber und 'nen leckeren Roten...


.....bis später...

 

[Ziegenpeter]

Also es ist 21:00…

@Serpel beim Schneeschippen verschüttet,
@achimL muss Klausuren korrigieren,
@willi.k leidet nach dem Gänsebraten bestimmt an postprandialer Somnolenz (),
@GSMilan segelt dankenswerter Weise im Schwarzwald und hält dadurch die Windradseuchepopulation im Zaum und
@nobbe wartet ungeduldig mit dem darauf den Weihachtsmann zu suchen.

Deshalb hier eine Lösung skizziert. @nobbe, dein Spiel.

 

[nobbe]

@nobbe, dein Spiel.

oh..
nur so mal zur entspannung von der weihnachtszeit

 

[Serpel]

Also es ist 21:00…

@Serpel beim Schneeschippen verschüttet,
...

Manno, du könntest auch ein bisschen geduldiger sein! So ein schönes Rätsel und ich erfahre erst nach Ablauf der Frist davon ...

Ich habe eine anderen Lösungsweg auf die Schnelle, vielleicht interessiert er dich. Muss erst noch ne Skizze malen ...

Gruß
Serpel

 

[Serpel]

Pythagoras sagt:

1 = (√2a)^2 + (a/√2)^2 = 2a^2 + a^2/2 = 5/2a^2

und daraus folgt:

a^2 = 2/5 = 0.4

Gruß
Serpel

 

[willi.k]

View attachment 454600

Danke, ein Genuss, das nachzuvollziehen.

 

[GSMilan]

@Ziegenpeter
Mein rudimentäres Gemale war fast ähnlich, sieh Anhang.
@Serpel
Saubere Lösung

 

[Ziegenpeter]

View attachment 454614

Pythagoras sagt:

1 = (√2a)^2 + (a/√2)^2 = 2a^2 + a^2/2 = 5/2a^2

und daraus folgt:

a^2 = 2/5 = 0.4

Gruß
Serpel

Noch schönere Lösung!

Die Knobelei war ja schon seit Mittwoch gepostet.

Aber hat auch was gutes wenn Serpel, Achim und iHans mal abgelenkt sind, ansonsten wird ja jede Knobelei oder Ortsuche innerhalb weniger Minuten gelöst…

 

[Ziegenpeter]

oh..
nur so mal zur entspannung von der weihnachtszeit

View attachment 454603

Was wird gesucht?

 

[gshogi]

Wahrscheinlich Katzen, Marsmännchen, Schneemänner, Drachen, Roboter, Yeti, Hunde, Pegasus, Einhörner,...

 

[Serpel]

Oder das kleine omikron.

Gruß
Serpel

 

[Ziegenpeter]

Darth Vader Rentier

 

[achimL]

@achimL muss Klausuren korrigieren,

Das zwar gerade nicht, aber die Woche war aus anderen, verschiedenen Gründen - sagen wir: gut gefüllt. Deshalb war ich nicht so oft hier und habe Dein schönes Rätsel total verpasst. Hätte aber auch keine Zeit gehabt, mich daran zu versuchen...Aber Ihr kommt auch gut ohne mich klar! (@Serpel: sehr elegante Lösung! )

 

[nobbe]

Was wird gesucht?

Einfach mal so.. jeder sagt was so auffällt

 

[gshogi]

Alles! Wirklich alles ist auffallend. Bis auf den Schnee. Ist ja schließlich eine Winterlandschaft.